원둘레 구하는 공식
😊 서론
수학에서 원은 아주 중요한 도형 중 하나죠! 원의 둘레와 넓이를 구하는 공식도 초등학교 때부터 배우기 시작해 익숙할 텐데요. 오늘은 중학교에서 배우는 원의 공식과 그 활용법에 대해 살펴보려고 합니다. 특히, 초등학교 때 배운 3.14 대신에 π를 사용하는 방법을 집중적으로 다뤄볼게요!
1. 원주율과 π
🎯 원주율의 개념
먼저, 원주율이라는 개념부터 복습해볼까요? 원주율은 원의 둘레와 지름의 비율을 의미해요. 즉, 원을 아무리 크게 만들거나 작게 만들어도, 원의 둘레는 지름에 항상 일정한 비율로 정해지죠. 이 비율을 π(파이)라고 부릅니다. 초등학교에서는 계산의 편의를 위해 3.14로 간단히 처리했지만, 이제는 더 정확한 수학적 기호인 π를 사용한답니다!
💡 π의 활용
π는 원을 계산할 때 가장 중요한 역할을 합니다. 원의 둘레와 넓이를 구하는 공식에서 π는 필수적으로 등장하죠. 그러면 이제 원의 둘레를 구하는 공식을 한번 확인해볼까요?
2. 원의 둘레 공식
📏 공식: l = 2πr
원의 둘레를 구하는 공식은 다음과 같아요: l = 2πr. 여기서 r은 원의 반지름, l은 원의 둘레입니다. 예를 들어, 반지름이 10cm인 원이 있다고 가정해볼게요. 이 원의 둘레는 2π × 10cm = 20π cm가 됩니다.
중학교에서는 3.14를 곱해 계산하지 않고, π를 그대로 사용해 표현하는 경우가 많아요. 이렇게 하면 계산이 간단해지죠!
원둘레 구하는 공식 - 🎯 예시로 이해하기
이번에는 실제로 원의 둘레를 구하는 예시를 통해 더 명확하게 이해해볼까요? 반지름이 5cm인 원의 둘레를 구해봅시다. 공식을 적용해보면,






l = 2πr = 2π × 5 = 10π cm
아하, 결과는 10π cm이네요! 이렇게 π를 그대로 사용하면 계산이 훨씬 간단해집니다. 만약 굳이 3.14로 계산한다면,
10 × 3.14 = 31.4 cm
라고 나오지만, π를 그대로 쓰면 계산할 필요 없이 더 깔끔하게 정리할 수 있답니다!
원둘레 구하는 공식 - 💡 주의할 점!
공식을 사용할 때 주의해야 할 점이 있어요. 바로 반지름과 지름을 헷갈리지 않는 것이죠! 원의 지름은 반지름의 2배입니다. 따라서 만약 지름이 주어졌다면 반지름을 먼저 계산한 후 둘레를 구해야 해요. 예를 들어, 지름이 12cm인 원이 있다면 반지름은 6cm겠죠? 그 다음에 이 반지름을 가지고 둘레를 구하는 거예요!
3. 원의 넓이 공식
🌟 넓이 공식: S = πr²
원의 넓이 공식도 한번 알아볼까요? 원의 넓이는 S = πr²로 구할 수 있어요. 이 공식에서 r은 역시 반지름이고, π는 우리가 앞서 다뤘던 π입니다. 예를 들어, 반지름이 7cm인 원의 넓이를 구해볼게요. 그러면,
S = π × (7cm)² = 49π cm²
이렇게 원의 넓이는 49π cm²로 표현할 수 있답니다!
💡 원 넓이 예시
이번에는 조금 더 복잡한 예시를 살펴볼게요. 반지름이 12cm인 원의 넓이를 구해봅시다. 공식에 반지름을 대입하면,
S = π × (12cm)² = π × 144 = 144π cm²
따라서, 이 원의 넓이는 144π cm²가 됩니다. 이렇게 π를 사용해 표현하면 계산 과정이 간단해지죠! 만약 3.14로 바꾸어 계산하면,
144 × 3.14 = 452.16 cm²
이렇게도 구할 수 있지만, π를 그대로 남겨두면 더 깔끔하고 편리하게 사용할 수 있어요.

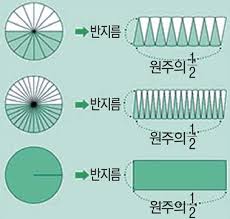




⚡ 원의 넓이와 둘레 비교
원의 둘레와 넓이를 구하는 공식은 다소 비슷해 보일 수 있지만, 사실 서로 다른 개념을 표현하고 있답니다. 원의 둘레는 원의 가장자리를 따라 그린 선의 길이, 반면에 원의 넓이는 그 내부의 공간 크기를 의미하죠.
둘 다 π를 사용해 계산하지만, 둘레는 l = 2πr, 넓이는 S = πr²로 다르게 계산한다는 점을 꼭 기억하세요! ^^
4. 부채꼴의 호의 길이와 넓이
🎯 부채꼴에서 호의 길이 구하기
원의 일부인 부채꼴에서도 둘레와 넓이를 구할 수 있어요. 부채꼴의 호의 길이는 원의 둘레에서 일정한 비율을 차지하게 되죠. 이를 계산하는 공식은 다음과 같습니다:
l = 2πr × x ÷ 360
여기서 x는 중심각의 크기(°)입니다. 즉, 전체 원 둘레에서 중심각의 비율만큼을 곱해주면 부채꼴의 호의 길이를 구할 수 있어요!
💡 부채꼴 호의 길이 예시
예를 들어, 반지름이 8cm이고 중심각이 90°인 부채꼴의 호의 길이를 구해볼게요. 공식을 적용하면,
l = 2π × 8 × 90 ÷ 360 = 4π cm
따라서, 이 부채꼴의 호의 길이는 4π cm입니다. 마찬가지로 π를 사용하여 간단하게 계산할 수 있죠!


🌟 부채꼴 넓이 구하기
부채꼴의 넓이는 원의 넓이에서 일정 부분만 차지하는 방식으로 계산됩니다. 공식은 다음과 같습니다:
S = πr² × x ÷ 360
여기서도 x는 중심각의 크기(°)입니다. 부채꼴의 넓이는 원의 넓이에서 중심각의 비율만큼을 곱해서 구해요.
💡 부채꼴 넓이 예시
반지름이 8cm이고 중심각이 90°인 부채꼴의 넓이를 구해볼까요? 공식을 적용하면,
S = π × (8cm)² × 90 ÷ 360 = 16π cm²
따라서, 이 부채꼴의 넓이는 16π cm²입니다. 이렇게 부채꼴의 넓이도 π를 사용해 쉽게 구할 수 있어요!
원둘레 구하는 공식 - 결론
오늘은 원의 둘레와 넓이, 그리고 부채꼴의 호의 길이와 넓이를 구하는 공식을 배워보았습니다. 😊 수학 공식은 정확히 알고 있으면 어렵지 않답니다. π를 사용하면 계산이 훨씬 간단해지니, 이제부터는 3.14 대신 π를 이용해 더 빠르고 간편하게 계산해보세요! ^^
신선초 효능 섭취시 주의사항
신선초 효능 알아보기!안녕하세요~ 오늘은 건강에 좋은 식물로 잘 알려진 신선초에 대해 알아보려고 해요! 신선초는 다양한 효능을 가지고 있어서, 건강을 챙기고자 하는 분들에게 많은 사랑을
wiki.longlivearea.com